Beat Detection Algorithms (Part 2)

This post describes the second part of my journey in the land of beat detection algorithms. In the first part I presented two fast but rather inaccurate algorithms that could be used for beat and tempo detection when performance is much more important than precision. In this post I will present an algorithm (and its implementation) that is more complex (to understand, to code and to run) but that provides incredibly accurate results on every audio file I tested it on.

The algorithm was originally proposed by George Tzanetakis, Georg Essl and Perry Cook in their 2001 paper titled Audio Analysis using the Discrete Wavelet Transform. You can find an implementation of the algorithm in the class WaveletBPMDetector in the Scala scala-audio-file library.
Please notice that so far the library is only able to process WAV files.

###Discrete Wavelet Transform

To detect the tempo of a song the algorithm uses the Discrete Wavelet Transform (DWT). A lot could be said on data transformations but this is a bit out of the scope of this post. In the field of audio processing, the DWT is used to transform data from the time domain to the frequency domain (and vice versa). When compared to the widely used Fast Fourier Transfor (FFT), the DWT allows to switch to the frequency domain while keeping information on the time location at several levels of granularity. Roughly speaking, the discrete wavelet transform applies combined low pass and high pass filters and produces some approximation and detail coefficients respectively.

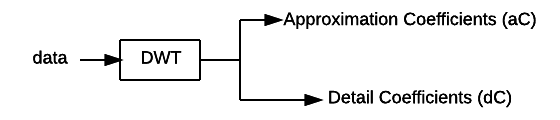
Cascading application of DWT can be applied to increase the frequency resolution of the approximation coefficients thus isolating different frequency sub-bands. For a more correct/precise/detailed description of the discrete wavelet transform have a look at the Wikipedia page.

###The Algorithm

The algorithm divides an audio file into windows of frames. The size of each window should correspond to 1-10 seconds of the original audio. For the sake of simplicity we consider a single-channel (mono) track, but the algorithm can be easily applied to stereo tracks as well. Audio data (data) of a window is processed through the discrete wavelet transform and divided into 4 frequency sub-bands (4 cascading applications of DWT).

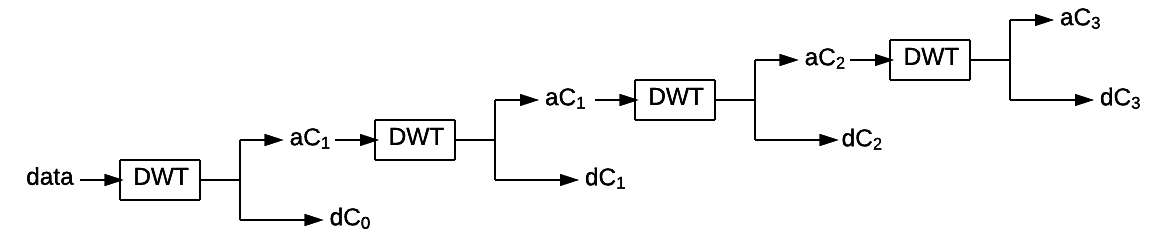
For each frequency sub-band (i.e. its detail coefficients \(dC\)) an envelope is computed. Envelopes are obtained through the following operations:

1. Full wave rectification: take the absolute value of the coefficients \[ dC’[j] = | dC[j] | ~~~\forall j\]
2. Downsampling \[ dC’‘[j] = dC’[k \cdot j] ~~~\forall j\]
3. Normalization: subtract the mean \[ dC’'’i[j] = dC’‘[j] - mean(dC’‘[j]) ~~~\forall j\]

Envelopes are then summed together (in \(dCSum\)) and autocorrelation is applied to the just computed sum.

\[ correl[k] = \sum _ j dCSum[j] \cdot dCSum[j+k] ~~~\forall k\]

A peak in the autocorrelated data corresponds to a peak in the signal envelope, that is, a peak in the original data. The maximum value in the autocorrelated data is therefore identified and from its position the approximated tempo of the whole window is computed and stored.

Once all windows are processed the tempo of the track in beats-per-minute is returned as the median of the windows values.

###Implementation

The algorithm is implemented by the class WaveletBPMDetector in the Scala scala-audio-file library. Objects of the class can be constructed through the companion object by providing:

• An audio file
• The size of a window in number of frames
• The type of wavelet

So far only Haar and Daubechies4 wavelets are supported. To evaluate the algorithm add the scala-audio-file library to your project and instantiate the WaveletBPMDetector class as:

val file = WavFile("filename.wav")
val tempo = WaveletBPMDetector(
              file, 
              131072, 
              WaveletBPMDetector.Daubechies4).bpm

###Evaluation

I gave a try to the algorithm/implementation on the release “The Seven Fluxes” that you can find on Beatport. I am developing these algorithms to integrate them in a music store so I expect the user not to be very interested in decimal digits. I take as a reference the tempos provided by Beatport. I am not actually expecting them to be the correct tempo of the track but due to the type of application that will use the algorithm I am satisfied of providing as accurate results as the N.1 store for electronic music. Only the first 30 seconds of each track are used to detect the tempo.

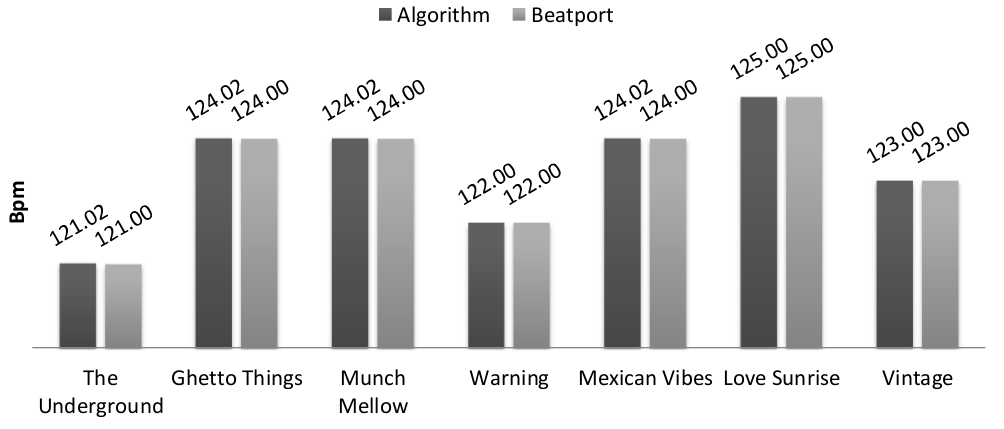
The results show that the algorithm provides the exact same results as Beatport, which is quite cool.

To be fair, the tracks are tech/house music and this makes the task of beat detection easier. A more thorough evaluation of the algorithm is given in the original paper.

###Important Notes

• If necessary, the precision of the algorithm can be increased by dividing the data into more than 4 sub-bands (by using more cascading applications of DWT)

• Due to the way the DWT is implemented the size of a window in number of frames must be a power of two. In the example, 131072 approximately corresponds to 3 seconds of an audio track sampled at 44100Hz

• Algorithm implementation could be notably faster. Autocorrelation is in fact performed through brute force and has a \( O(n^2) \) running time. \( O(n \cdot log(n)) \) algorithms for autocorrelation exist as well, I will implement one of them as soon as possible

• The implementation works on stereo signal but detects only beats
  in the first channel. I still have to figure out how to exploit multiple channels data (max/avg/sum?), as soon as I identify a reasonable approach I will update the implementation (suggestions are appreciated)