10 Aug 2015
UPDATE: Benchmark results of Node-TimSort with Node.js v4.1.1 available
here.
TimSort is an adaptive and stable sort algorithm based on merging that requires fewer than nlog(n)
comparisons when run on partially sorted arrays. The algorithm uses O(n) memory and still runs in O(nlogn)
(worst case) on random arrays.
I implemented TimSort for Node.js in the timsort module, which is avalaible on
Github and npm.
The implementation is based on the original
TimSort developed
by Tim Peters for Python’s lists (code here).
TimSort has been also adopted in Java starting from version 7.
To study the performance of the implementation I wrote a benchmark which is available
on Github at benchmark/index.js.
It compares the timsort module against
the default array.sort method in the numerical sorting of different types of integer array
(as described here):
- Random array
- Descending array
- Ascending array
- Ascending array with 3 random exchanges
- Ascending array with 10 random numbers in the end
- Array of equal elements
- Random Array with many duplicates
- Random Array with some duplicates
For any of the array types the sorting is repeated several times and for
different array sizes, average execution time is then printed.
I run the benchmark on Node v0.12.7 (both pre-compiled and compiled from source,
results are very similar), obtaining the following values:
| |
Execution Time (ns) |
Speedup |
| Array Type |
Length |
TimSort.sort |
array.sort |
| Random |
10 | 2374 | 4256 | 1.79 |
| 100 | 12709 | 45903 | 3.61 |
| 1000 | 134876 | 479581 | 3.56 |
| 10000 | 1724563 | 6485514 | 3.76 |
| Descending |
10 | 1637 | 2869 | 1.75 |
| 100 | 2631 | 21267 | 8.08 |
| 1000 | 9330 | 352918 | 37.83 |
| 10000 | 74009 | 5114658 | 69.11 |
| Ascending |
10 | 1654 | 1751 | 1.06 |
| 100 | 2596 | 20159 | 7.77 |
| 1000 | 8253 | 340309 | 41.23 |
| 10000 | 60613 | 5045549 | 83.24 |
| Ascending + 3 Rand Exc |
10 | 1815 | 1981 | 1.09 |
| 100 | 4126 | 20564 | 4.98 |
| 1000 | 11490 | 342398 | 29.80 |
| 10000 | 85632 | 5062110 | 59.11 |
| Ascending + 10 Rand End |
10 | 2001 | 2410 | 1.20 |
| 100 | 6106 | 23537 | 3.85 |
| 1000 | 17195 | 337073 | 19.60 |
| 10000 | 99977 | 4868866 | 48.70 |
| Equal Elements |
10 | 1581 | 1710 | 1.08 |
| 100 | 2492 | 4562 | 1.83 |
| 1000 | 7337 | 31360 | 4.27 |
| 10000 | 50090 | 311882 | 6.23 |
| Many Repetitions |
10 | 1966 | 2415 | 1.23 |
| 100 | 15115 | 25965 | 1.72 |
| 1000 | 182287 | 372412 | 2.04 |
| 10000 | 2382618 | 5317724 | 2.23 |
| Some Repetitions |
10 | 1994 | 2549 | 1.28 |
| 100 | 14432 | 25101 | 1.74 |
| 1000 | 181708 | 364835 | 2 |
| 10000 | 2351346 | 5149683 | 2.19 |
TimSort.sort is faster than array.sort on any of the tested array types.
In general, the more ordered the array is the better TimSort.sort performs with respect to array.sort (up to 80 times faster on already sorted arrays).
And also, the bigger the array the more we benefit from using
the timsort module.
These data strongly depend on Node.js version and the machine on which the benchmark is run.
I strongly encourage you to clone the repository and run the benchmark on your own setup with:
Please also notice that:
- This benchmark is far from exhaustive. Several cases are not considered
and the results must be taken as partial
- inlining is surely playing an active role in
timsort module’s good performance
- A more accurate comparison of the algorithms would require implementing
array.sort in pure javascript
and counting element comparisons
array.sort will probably still be faster at lexicographically sorting
arrays of numbers. In this case, the timsort module inefficiently converts
values to strings inside the compare function and then compares the strings.
array.sort, instead, uses a smarter and faster lexicographic
comparison of numbers (will try to do something similar soon).
Stability
TimSort is stable which means that equal items maintain their relative order
after sorting. Stability is a desirable property for a sorting algorithm.
Consider the following array of items with an height and a weight.
[
{ height: 100, weight: 80 },
{ height: 90, weight: 90 },
{ height: 70, weight: 95 },
{ height: 100, weight: 100 },
{ height: 80, weight: 110 },
{ height: 110, weight: 115 },
{ height: 100, weight: 120 },
{ height: 70, weight: 125 },
{ height: 70, weight: 130 },
{ height: 100, weight: 135 },
{ height: 75, weight: 140 },
{ height: 70, weight: 140 }
]
Items are already sorted by weight. Sorting the array
according to the item’s height with the timsort module
results in the following array:
[
{ height: 70, weight: 95 },
{ height: 70, weight: 125 },
{ height: 70, weight: 130 },
{ height: 70, weight: 140 },
{ height: 75, weight: 140 },
{ height: 80, weight: 110 },
{ height: 90, weight: 90 },
{ height: 100, weight: 80 },
{ height: 100, weight: 100 },
{ height: 100, weight: 120 },
{ height: 100, weight: 135 },
{ height: 110, weight: 115 }
]
Items with the same height are still sorted by weight which means they preserved their relative order.
array.sort, instead, is not guarranteed to be stable. In Node v0.12.7
sorting the previous array by height with array.sort results in:
[
{ height: 70, weight: 140 },
{ height: 70, weight: 95 },
{ height: 70, weight: 125 },
{ height: 70, weight: 130 },
{ height: 75, weight: 140 },
{ height: 80, weight: 110 },
{ height: 90, weight: 90 },
{ height: 100, weight: 100 },
{ height: 100, weight: 80 },
{ height: 100, weight: 135 },
{ height: 100, weight: 120 },
{ height: 110, weight: 115 }
]
As you can see the sorting did not preserve weight ordering for items with the
same height.
Usage
To use the module in you project install the package:
npm install --save timsort
And use it:
var TimSort = require('timsort');
var arr = [...];
TimSort.sort(arr);
As array.sort() by default the timsort module sorts according to
lexicographical order.
You can also provide your own compare function (to sort any object) as:
function numberCompare(a,b) {
return a-b;
}
var arr = [...];
var TimSort = require('timsort');
TimSort.sort(arr, numberCompare);
You can also sort only a specific subrange of the array:
TimSort.sort(arr, 5, 10);
TimSort.sort(arr, numberCompare, 5, 10);
19 Jun 2015
Scalability plays a key role in the success of an application/service. Being
able to remain responsive in the face of heavy loads is crucial
for a growing application.
A lot of effort is spent to design scalable systems with the aid of
state of the art paradigms, frameworks and tools.
Developing a scalable system is, however, only part of the solutions.
A system capable of scaling is of no use if we do not know when to
scale it. The point is that we want our services to
scale up/out when the load is intensifying but at the same time
we want to strongly avoid scaling up/out when not needed. Scaling,
in fact, never comes for free: additional resources mean additional
costs that we want to avoid if not really necessary.
To complicate this scenario, we might have committed to provide
our users with a specific service level
(e.g. through a Service Level Agreement).
In this cases we can not afford
to scale up/out when the load reaches critical levels but we rather
want to be proactive. That is, we scale up/out before the
Quality of Service offered to the users degrades. Proactiveness,
however, often leads to provisioning and non cost-effective
decisions.
I am currently working on a web application that does some
heavy sound processing (as beat detection that I discussed
here) on user-submitted audio files.
I want the processing service to scale proactively without ever
degrading user experience (avoid long wait times).
I am able to scale out these services but I don’t want to waste money
on unused resources so I was after some tool to aid me
predict the load on my system to more accurately decide when to scale.
Several tools allow engineers to monitor the resource
consumption (CPU, memory, network) and load of their systems. Few techniques however
are available to guide proactive scaling. Few tools, in fact,
help engineers and system designers to quantify possible future peaks
in their system’s workload. And almost none of such tools
provides a quantifiable confidence on the predicted peak.
Workload prediction
(as well as resource demand prediction) is often performed by experts on the basis
of time series and real-time information but is hardly guided by statistical/scientific
evidence.
In this scenario, Extreme Value Analysis can help predicting workload peaks
starting from time series and can therefore serve as a fruitful aid to proactive scaling.
Extreme Value Analysis
Extreme Value Analysis (EVA)
is a statistical theory that aims at assessing
the probability of extreme events given an ordered sample of a random variable.
EVA is applied in several fields as for instance, structural engineering, finance and
traffic prediction. Recent studies also apply EVA to the prediction of network congestions.
For practical applications of EVA, the Block Maxima technique can be used. With block
maxima the input time series is divided into blocks of fixed size from each of which only the
maximum value is taken. The resulting sample is called block maxima serer.
EVA then fits to the block maxima data a Generalized Extreme Value (GEV) distribution.
GEV distribution is a family of continuous distributions that approximates well the
behaviour of maximum values in a time series.
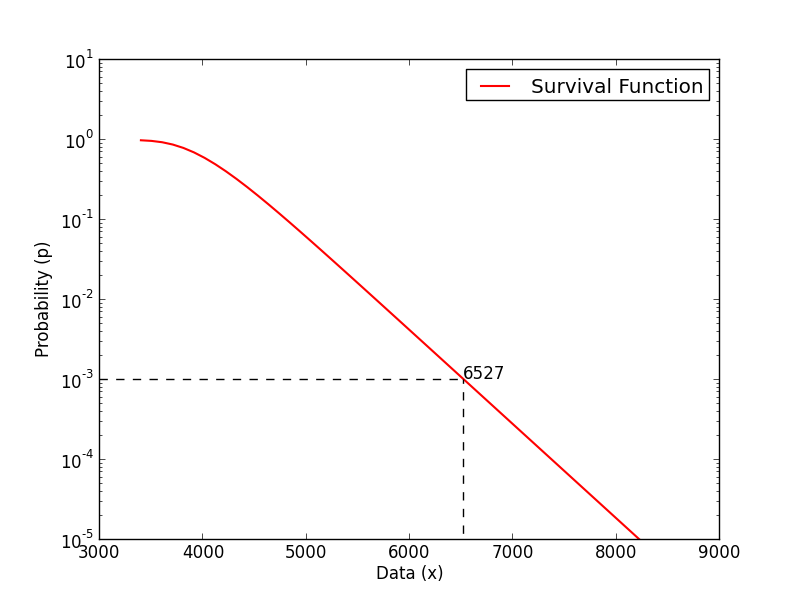
Once a GEV continuous distribution has been fit to the data a survival function can be
extracted from it. The survival function
(also known as reliability function or complementary cumulative distribution function)
says for any value x, the probability p
that a value higher than x occurs in the event represented by the original data.
As you can understand
with such a distribution we can choose a probability value p and extract
the corresponding value x such that the probability of
witnessing a value higher than x is p. That is, we
can not only identify peaks but also quantify the probability of exceeding them.
In figure above an example of a survival function is shown. As you can see
from the plot, the value 6527 is associated to the probability \(10^{-3}\)
which means that, in the event represented by the input time series,
the probability of observing values
that exceed 6527 is only \(10^{-3}\).
Predicting Workload
In the context of predicting workload peaks, the time series fed to Extreme Value
Analysis can represent either traffic load, memory consumption, CPU usage and so on.
Consider for instance traffic load, but the same reasoning also applies
to other metrics.
Given a time series representing traffic load we can apply EVA to that data.
Extreme Value Analysis fits to the block maxima a GEV continuous distribution.
From the corresponding survival function we are able
to extract traffic values that are only exceeded with arbitrarily low probabilities.
For instance, let’s pick a probability \(p = 10^{-3}\) and its corresponding
traffic load value x.
We now not only have a prediction of future traffic load but also the
probability that this prediction is exceeded.
Scaling up/out our service so that is can handle the traffic load x
means knowing that the probability of overloading the service is
\(p = 10^{-3}\). That is, 99.9% of uptime.
Example
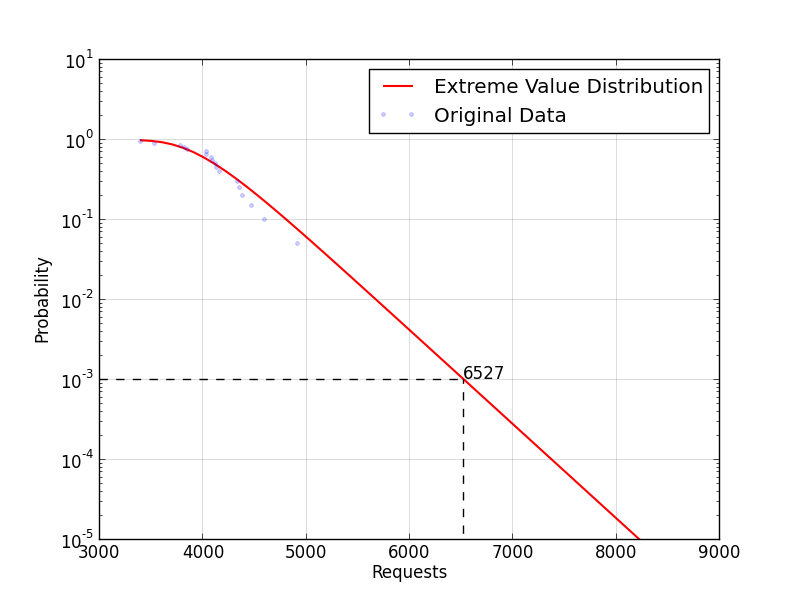
Consider as an example the following time series representing the
maximum daily number of simultaneous requests to a service (for the last 20 days):
[ 4352, 4472, 3847, 4915, 4969, 4333, 4381, 4091, 4135, 4160,
3534, 4598, 4086, 3788, 4038, 3396, 4118, 3822, 4333, 4034 ]
If we apply Extreme Value Analysis to that data we get the following
survival function:
Scaling out the service so that it can handle 6527 simultaneous
requests ensures us that it will be overloaded only with a
probability \(p = 10^{-3}\) which is a 99.9% daily uptime.
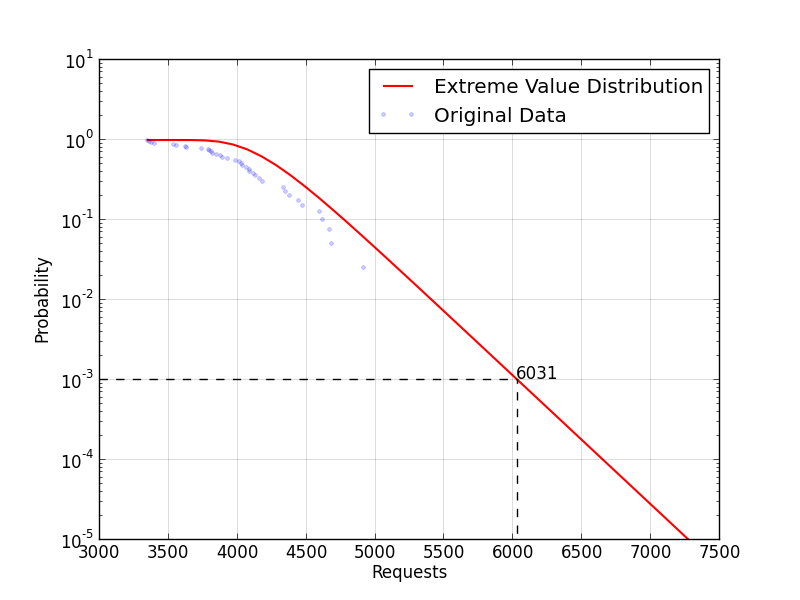
In addition, the more data we have, the more accurately
we can predict possible peaks. If we extend the previous
example data with other 20 values (for a total of 40 days):
[ 4352, 4472, 3847, 4915, 4969, 4333, 4381, 4091, 4135, 4160,
3534, 4598, 4086, 3788, 4038, 3396, 4118, 3822, 4333, 4034,
3738, 4670, 3346, 4070, 3556, 3810, 3984, 3892, 4615, 3634,
4016, 3378, 4441, 3800, 4182, 3879, 3926, 3625, 4687, 3366 ]
If we apply Extreme Value Analysis to that data we get the following
survival function:
That associates to \(p = 10^{-3}\) a lower workload value (6031).
Source Code
You can find the Python pyscale module that implements the
workload prediction on Github.
To predict a load peak at a given probability
you can instantiate an object of the class LoadPredictor as:
from pyscale import LoadPredictor
load_data = [ 4352, 4472, 3847, 4915, 4969, 4333, 4381, 4091, 4135, 4160,
3534, 4598, 4086, 3788, 4038, 3396, 4118, 3822, 4333, 4034 ]
predictor = LoadPredictor(load_data)
load_peak = predict_load(0.001)
You can also produce a plot of the survival function by instantiating an
object of the class PredictionPlotter:
from pyscale import LoadPredictor
load_data = [ 4352, 4472, 3847, 4915, 4969, 4333, 4381, 4091, 4135, 4160,
3534, 4598, 4086, 3788, 4038, 3396, 4118, 3822, 4333, 4034 ]
predictor = LoadPredictor(load_data)
plotter = PredictionPlotter(predictor)
plotter.xlabel('Requests')
plotter.ylabel('Probability')
plotter.plot("plot.png", 0.001)
Notes
I would like to compare the workloads predicted by this approach
with real load data of a growing web service. That would
allow me to really understand the cost impact of scaling when guided
by these predictions.
Unluckily, I don’t have real-word data for a thorough evaluation now
but I should have them reasonably soon (as soon as I get those data
I will update this post).
If you ever give a try to this approach and collect some data
from your services/applications please contact me as I would love to
have a look at the results.
12 Jun 2015
This post describes the second part of my journey in the land of beat detection algorithms.
In the first part I presented two fast but rather inaccurate algorithms
that could be used for beat and tempo detection when performance is much more important
than precision. In this post I will present an algorithm (and its implementation)
that is more complex (to understand, to code and to run) but that provides
incredibly accurate results on every audio file I tested it on.
The algorithm was originally proposed by George Tzanetakis, Georg Essl and Perry Cook in their 2001
paper
titled Audio Analysis using the Discrete Wavelet Transform.
You can find an implementation of the algorithm in the class WaveletBPMDetector in the Scala scala-audio-file library.
Please notice that so far the library is only able to process WAV files.
###Discrete Wavelet Transform
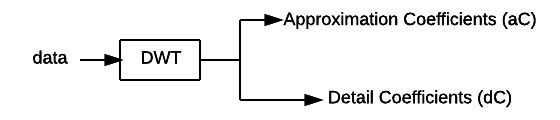
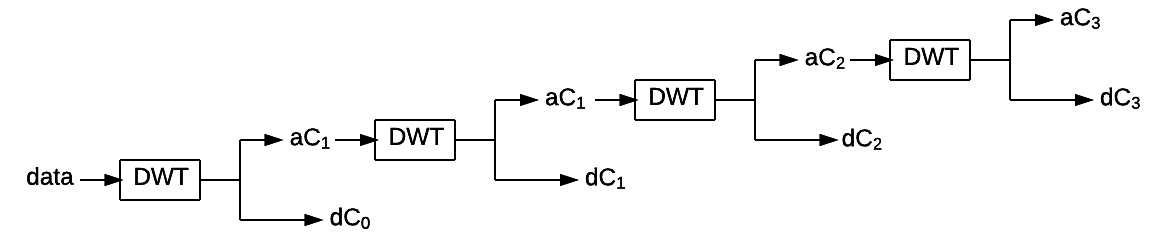
To detect the tempo of a song the algorithm uses the Discrete Wavelet Transform (DWT).
A lot could be said on data transformations but this is a bit out of the scope of this post.
In the field of audio processing, the DWT is used to transform data
from the time domain to the frequency domain (and vice versa). When compared to
the widely used Fast Fourier Transfor (FFT), the DWT allows to switch to the frequency
domain while keeping information on the time location at several levels
of granularity. Roughly speaking, the discrete wavelet transform applies
combined low pass and high pass filters and produces some
approximation and detail coefficients respectively.
Cascading application of DWT can be applied to increase the frequency
resolution of the approximation coefficients thus isolating different
frequency sub-bands.
For a more correct/precise/detailed description of the discrete wavelet transform
have a look at the Wikipedia page.
###The Algorithm
The algorithm divides an audio file into windows of frames.
The size of each window should
correspond to 1-10 seconds of the original audio. For the sake of simplicity
we consider a single-channel (mono) track, but the algorithm can be easily applied to stereo tracks as well.
Audio data (data) of a window is processed through the discrete
wavelet transform and divided into 4 frequency sub-bands (4 cascading
applications of DWT).
For each frequency sub-band
(i.e. its detail coefficients \(dC\)) an envelope is
computed. Envelopes are obtained through the following operations:
- Full wave rectification: take the absolute value of the coefficients
\[ dC’[j] = | dC[j] | ~~~\forall j\]
- Downsampling
\[ dC’‘[j] = dC’[k \cdot j] ~~~\forall j\]
- Normalization: subtract the mean
\[ dC’'’i[j] = dC’‘[j] - mean(dC’‘[j]) ~~~\forall j\]
Envelopes are then summed together (in \(dCSum\)) and
autocorrelation is applied to the just computed sum.
\[ correl[k] = \sum _ j dCSum[j] \cdot dCSum[j+k] ~~~\forall k\]
A peak in the autocorrelated data corresponds to a peak in the
signal envelope, that is, a peak in the original data.
The maximum value in the autocorrelated data is therefore
identified and from its position the approximated
tempo of the whole window is computed and stored.
Once all windows are processed the tempo of the track
in beats-per-minute is returned as the median of the windows values.
###Implementation
The algorithm is implemented by the class WaveletBPMDetector
in the Scala scala-audio-file library. Objects of the class can be constructed through the companion
object by providing:
- An audio file
- The size of a window in number of frames
- The type of wavelet
So far only Haar and Daubechies4 wavelets are supported.
To evaluate the algorithm add the
scala-audio-file library
to your project and instantiate the WaveletBPMDetector class as:
val file = WavFile("filename.wav")
val tempo = WaveletBPMDetector(
file,
131072,
WaveletBPMDetector.Daubechies4).bpm
###Evaluation
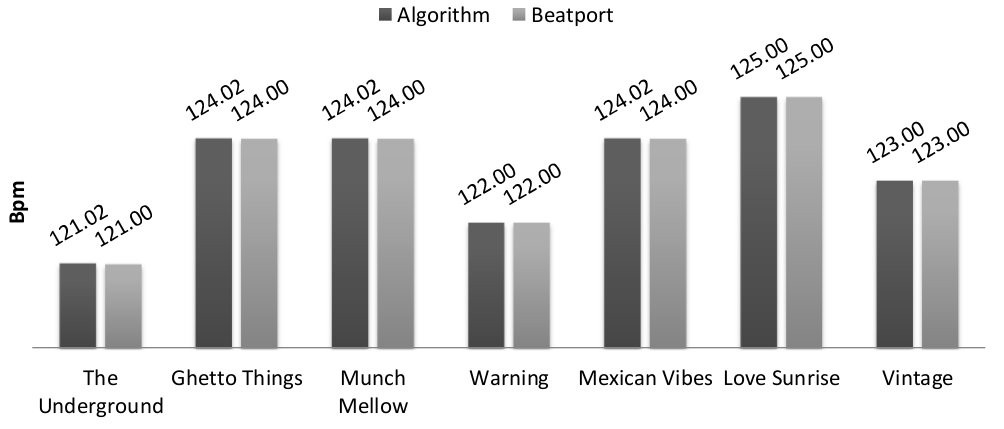
I gave a try to the algorithm/implementation on the release “The Seven
Fluxes” that you can find on
Beatport.
I am developing these algorithms to integrate them in a music
store so I expect the user not to be very interested in decimal digits.
I take as a reference the tempos provided by Beatport. I am not actually
expecting them to be the correct tempo of the track but due to the type
of application that will use the algorithm I am satisfied of providing
as accurate results as the N.1 store for electronic music.
Only the first 30 seconds of each track are used to detect the tempo.
The results show that the algorithm provides the exact same results
as Beatport, which is quite cool.
To be fair, the tracks are tech/house music and this makes the task
of beat detection easier. A more thorough evaluation of the algorithm
is given in the original
paper.
###Important Notes
-
If necessary, the precision of the algorithm can be increased by
dividing the data into more than 4 sub-bands (by using more cascading
applications of DWT)
-
Due to the way the DWT is implemented the size of a window in number of
frames must be a power of two. In the example, 131072 approximately
corresponds to 3 seconds of an audio track sampled at 44100Hz
-
Algorithm implementation could be notably faster. Autocorrelation
is in fact performed through brute force and has a \( O(n^2) \) running
time. \( O(n \cdot log(n)) \) algorithms for autocorrelation exist
as well, I will implement one of them as soon as possible
-
The implementation works on stereo signal but detects only beats
in the first channel. I still have to figure out how to exploit
multiple channels data (max/avg/sum?), as soon as I identify
a reasonable approach I will update the implementation (suggestions
are appreciated)
28 May 2015
You can think to the beat of a song as the rythm you tap your foot at while
listening to it. The tempo of a song is usually measured in beats per minute.
The tempo of a song, its beats, are usually felt by a listener and drive him,
for instance, to dance according to the song’s rythm. As it is often the case,
things that a human can feel are not easy to detect through a computer
program. This is the first of 2 posts on beat detection algorithms in which I introduce
two simple algorithms I implemented in Scala scala-audio-file library.
Please notice that so far the library is only able
to process WAV files.
###Sound Energy Algorithm
The first algorithm I will talk about was originally presented
here. I implemented it in the class
SoundEnergyBPMDetector.
The algorithm divides the data into blocks of samples and compares the energy
of a block with the energy of a preceding window of blocks.
The energy of a block is used to detect a beat. If the energy is above a certain
threshold then the block is considered to contain a beat.
The threshold is defined starting from the average energy of the window of
blocks preceding the one we are analyzing.
If a block j is made of 1024 samples and the song is stereo, its energy can be computed as:
\[ E _ j = \sum _ {i=0} ^ {1023} left[i]^2 + right[i]^2 \]
The block’s energy is then placed in a circular buffer
that stores all the energy values for the current window. Let us assume that
the current window is made of 43 blocks (\(43 \cdot 1024 = 44032\) ~ \(1s\) with a sample rate of \(44100\)), the average window energy can be computed as:
\[ avg(E) = \frac{1}{43} \sum _ {j=0} ^ {42} E _ j \]
We detect a beat if the instant energy \(E _ j\) is bigger than \(C \cdot avg(E)\).
In the original article, a
way to compute \(C\) is proposed as a linear regression of the energy variance in the corresponding window.
In the SoundEnergyBPMDetector
class
I use a slightly modified equation that lowers the impact of variance:
\[ C = -0.0000015 \cdot var(E) + 1.5142857 \]
In general, however, the bigger the variance the more likely we consider a
block to be a beat. The variance inside a window of blocks is defined as:
\[ var(E) = \frac{1}{43} \sum _ {j=0} ^ {42} (avg(E) - E _ j)^2 \]
This first algorithm is very easy to implement and fast to execute.
However, the results computed are rather imprecise. To evaluate it add the
scala-audio-file library
to your project and instantiate the SoundEnergyBPMDetector class as:
val audioFile = WavFile("filename.wav")
val tempo = SoundEnergyBPMDetector(audioFile).bpm
###Low Pass Filter Algorithm
This second algorithm is based on a
post
originally hosted on Beatport’s engineering blog by Joe Sullivan.
The original article uses the
Web Audio Api
to implement browser-side beat detection. A similar but more extensible
implementation of the algorithm is provided by the class FilterBPMDetector.
First, the algorithm applies to sampled data a biquad low-pass filter
(implemented by the class BiquadFilter). Filter’s parameters are computed
according to the “Cookbook formulae for audio EQ biquad filter coefficients”
by Robert Bristow-Johnson.
Filtered audio data are divided into windows of samples (whose dimension is
the sample frequency, i.e. 1s). A peak detection
algorithm is applied to each window and identifies as peaks
all values above a certain threshold (defined as \(C \cdot avg(window)\) where \(C\)
is for the user to be configured, e.g. \(0.95\)).
For each peak the distance in number of samples between it and its neighbouring
peaks is stored (10 neighbours are considered).
For each distance between peaks the algorithm counts how many times it has been detected across all windows in the song.
Once all windows are processed the algorithm has built a map distanceHistogram
where for each possible distance its number of occurrences is stored:
distanceHistogram(distance) = count
For each distance a theoretical tempo can be computed according to the
following equation:
\[ theoreticalTempo = 60 / (distance / sampleRate) \]
Here the algorithm builds on the assumption that the actual tempo of the song
lies in the interval [90, 180]. Any bigger theoretical tempo is divided by 2
until it falls in the interval. Similarly, any smaller tempo is multiplied by 2.
By converting each distance to the corresponding theoretical tempo
a map tempoHistogram is built where each tempo is
associated the sum of occurrences of all distances that lead to it:
tempoHistogram(tempo) = count
The algorithm computes the tempoHistogram map and selects as
the track’s tempo the one with the highest count.
This second algorithm is also very fast and provides better results than
the first one. To evaluate it, add the
scala-audio-file library
to your project and instantiate the FilterBPMDetector class as:
val audioFile = WavFile("filename.wav")
val filter = BiquadFilter (
audioFile.sampleRate,
audioFile.numChannels,
FilterType.LowPass)
val detector = FilterBPMDetector(audioFile, filter)
val tempo = detector.bpm
Conclusion
To sum things up, both algorithms are very fast to implement and execute. The
second one is a bit slower but provides better approximations of the actual
tempo. More time consuming algorithms that compute almost exact
results can be developed by exploiting the Fast Fourier Transform or the Discrete Wavelet Transform.
I will discuss such algorithms in the next post.
18 May 2015
I have been struggling to override the Content-Disposition and Content-Type
headers of Google Cloud Storage and Amazon S3 responses.
As you might know both S3 and
Cloud Storage let you generate signed URLs
(possibly set to expire in a specified amount of time)
to access stored objects. Signed URLs are often used to grant
non-authenticated users temporary access to otherwise private objects.
When the user opens a signed URL you may want the browser to download the object
rather than trying to render it.
It might as well be the case that the name you identify the object with
is not the name you want the user to see when downloading the file.
The Content-Disposition header of a response, if set properly, can
tell the browser to download the object and can even set a default filename
in the SaveAs prompt.
The question is: how do I set the Content-Disposition header of S3 and Storage responses?
Digging into Amazon’s and Google’s documentation I found the
response-content-disposition parameter: if added to a signed URL
it overrides the Content-Disposition header of the response allowing,
for instance, to show a SaveAs prompt when accessing the object.
Given a signed URL, you can override
the Content-Disposition to download the file as newfile.ext2:
<signed URL>&response-content-disposition=attachment; filename="newfile.ext2"
More details on Content-Disposition header’s format can
can be found here.
If you are interested, it is also possible to override the Content-Type header
of a response by providing the response-content-type parameter.
Please notice that both response-content-disposition and
response-content-type parameters must not be part of URL’s signature,
they can be simply appended once the URL has been signed.